Важнейшие результаты научных исследований за 2005 г. Математика, механика, информатика.

АЛГЕБРА, ТЕОРИЯ ЧИСЕЛ И МАТЕМАТИЧЕСКАЯ ЛОГИКА. Доказана квазираспознаваемость по множеству порядков элементов конечных простых групп исключительного лиева типа с несвязным графом простых чисел. (Институт математики и механики).
 

ГЕОМЕТРИЯ И ТОПОЛОГИЯ. Построено непрерывное открытое отображение прямой Зоргенфрея на вещественную прямую. Прямая Зоргенфрея – классический контрпример, являющийся объектом пристального внимания в общей топологии на протяжении последних десятилетий. Полученный результат важен для понимания связи между прямой Зоргенфрея и вещественной прямой. (Институт математики и механики).
 

МАТЕМАТИЧЕСКИЙ АНАЛИЗ. Для производной любого порядка найдена наилучшая константа в предельном случае (ρ → +0) неравенства Маркова – Никольского разных метрик для алгебраических многочленов на отрезке, что позволяет исследовать и другие аналогичные задачи. Результат важен для теории функций и ее приложений, например, при кодировании информации. (Институт математики и механики).
 

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА. Предложен метод построения уравнений разветвления при нахождении условий существования периодических решений для систем дифференциальных уравнений с последействием. Используя понятие квазилинейной системы, удалось рассмотреть с единых позиций бифуркации Ляпунова—Пуанкаре и Андронова—Хопфа. Применение специального интегрального уравнения позволило получить удобное представление уравнения разветвления, не привязывая его к конкретной вычислительной схеме. Рассматриваемая методика результативно использована при изучении бифуркаций Андронова—Хопфа в различных системах с запаздываением.
 

Для приближенного решения сингулярно возмущенной задачи с точкой поворота применена разностная схема экспоненциальной подгонки на сетке с постоянным шагом. Доказана равномерная по параметру возмущения сходимость решений, полученных по этой схеме, к решению исходной дифференциальной задачи с первым порядком точности.
 

Для систем уравнений в частных производных определено понятие "отображение, допускаемое системой", обобщающее понятие допускаемой системой группы симметрий. Определена категория дифференциальных уравнений в частных производных, объектами которой являются уравнения и системы уравнений, а морфизмами - допустимые отображения. Исследована категория параболических уравнений второго порядка, определенных на произвольных многообразиях. Разработана алгебраическая структура этой категории. Предложен специальный язык для описания и исследования структур такого типа для произвольных подкатегорий категории дифференциальных уравнений.
 

Рассмотрены сеточные аппроксимации краевой задачи на отрезке для сингулярно возмущенного параболического уравнения конвекции-диффузии с кусочно-гладким начальным условием, когда производная первого порядка начальной функции терпит разрыв I рода в угловой точке. При малых значениях параметра в окрестности характеристики предельного уравнения, выходящей из этой точки, и в окрестности выходной части границы возникают переходный и пограничный слои. Построены специальные разностные схемы, аппроксимирующие ε равномерное решение задачи, а также диффузионный поток и производную по пространственной переменной (вне окрестности погранслоя).
 

Рассмотрена траектория движения материальной точки в поле тяготения двух тел (с соотношение масс ε << 1), вращающихся вокруг своего центра масс по круговым орбитам. При прохождении точки вблизи тела малой массы характер траектории резко меняется, а ее асимптотика при ε → 0 имеет сложный характер. Построено и обосновано равномерное асимптотическое разложение траектории на протяжении всего пути с точностью до любой степени ε. В частности, указан алгоритм нахождения предельного значения угла поворота траектории после прохождения материальной точкой окрестности малой массы. (Институт математики и механики).
 

ПАРАЛЛЕЛЬНЫЕ И РАСПРЕДЕЛЕННЫЕ ВЫЧИСЛЕНИЯ. Построена программная модель разделенных неструктурированных двух- и трехмерных сеток с ячейками произвольной формы, предназначенная для разработки широкого класса параллельных алгоритмов сеточных методов. Основной особенностью модели является обеспечение динамической балансировки нагрузки и поддержка различных стратегий перераспределения и коммуникаций сеточных объектов. Результаты позволят повысить эффективность использования многопроцессорных вычислительных систем. (Институт прикладной механики).
 

УПРАВЛЕНИЕ ДВИЖУЩИМИСЯ ОБЪЕКТАМИ. СИСТЕМЫ НАВИГАЦИИ, ОРИЕНТАЦИИ И НАВЕДЕНИЯ. Установлена нечувствительность по результату к малым помехам и ослаблению геометрических ограничений задач управления с непрерывным функционалов качества, удовлетворяющих условию обобщенной единственности. Для задач, неудовлетворяющих этому условию по результату приведен соответствующий контрпример.
 

Для дифференциальной игры, в которой функционалом платы является время до попадания точки на целевое множество, получены достаточные условия совпадения заданной разрывной функции с функцией цены игры. Условия формулируются в терминах понятий u- и v-стабильных функций, хорошо изученных в теории позиционных дифференциальных игр и теории обобщенных минимаксных решений уравнений в частных производных первого порядка. Дополнительно требуется выполнение введенного в работе условия корректной сжимаемости множеств уровня тестируемой функции. Показано, что такое условие корректной сжимаемости не является избыточным. (Институт математики и механики).
 

РОБОТОТЕХНИКА И АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ. Разработана методика совместной оптимизации алгоритмов ориентации для бесплатформенных инерциальных навигационных систем (БИНС) и архитектур функционально-ориентированных процессоров (ФОП). На базе методики создан экспериментальный образец ФОП для реализации алгоритмов БИНС в составе малогабаритных высокоманевренных летательных аппаратов. Создан и запущен программно-аппаратный имитатор, предназначенный для разработок и исследований алгоритмов, программ и аппаратуры БИНС, включая инерциальные датчики. (Институт машиноведения).
 

МАТЕМАТИЧЕСКИЕ ПРОБЛЕМЫ МЕХАНИКИ И ИССЛЕДОВАНИЯ КОСМОСА. Для двух задач из неголономной механики (задачи о шаре Чаплыгина и задачи Веселовой) найдено представление в виде обобщенных систем Чаплыгина, которые могут быть проинтегрированы с помощью метода приводящего множителя. Рассмотрены обобщения двух указанных задач и предложены новые способы реализации неголономных связей. Указан ряд неголономных систем, обладающих инвариантной мерой и достаточным числом первых интегралов, для которых вопрос о гамильтоновой форме, даже после замены времени, остается открытым. Доказана теорема об изоморфизме динамики шара Чаплыгина и движения тела в жидкости для случая Клебша. (Институт математики и механики).
 

ОБЩАЯ МЕХАНИКА. Разработаны физико-химические основы и концепция механохимической модели полирования прецизионных изделий машиностроения из сталей с аустенитно-мартенситной структурой с трибохимически активными абразивными материалами на основе твердых растворов оксидов переходных металлов. Установлено, что полирование металлов с получением шероховатости поверхности R_z = 0,04-0,07 мкм является трибохимическим процессом, состоящим из двух стадий. В первую стадию происходит образование оксидной пленки на поверхности металла в результате ее активирования трением, во вторую – разрушение и удаление оксидной пленки. Показано, что скорость полирования зависит от трибохимической активности абразивного порошкового материала, причем для получения высоких классов (13-14) чистоты обработки поверхности абразивный материал должен содержать тонкодисперсные фракции, способные участвовать в трибохимических реакциях. (Институт машиноведения).
 

Обнаружен эффект транспортирования подвешенного на струне пьезоэлектрического осциллятора и установлен механизм этого движения. Разработаны конструкции нового типа реверсивных двигателей, реализующие открытый эффект. (Институт прикладной механики).
 

МЕХАНИКА ЖИДКОСТИ, ГАЗА И ПЛАЗМЫ, ТВЕРДОГО ТЕЛА, НЕИДЕАЛЬНЫХ И МНОГОФАЗНЫХ СРЕД. Предложена параметризация мелкомасштабной спиральной турбулентности для использования в численных метеорологических моделях с целью диагностики и прогноза предтайфунных состояний тропической атмосферы.
 

Построена логически непротиворечивая кинематика упруго-неупругого процесса при конечных деформациях.
 

Обнаружены автоколебательные режимы массообмена между каплей и раствором поверхностно-активного вещества (ПАВ). Выяснено, что причиной периодической интенсификации массопереноса является конвекция Марангони, генерирующая в растворе вблизи капли интенсивное двухвихревое течение. При этом период интенсификации движения составляет секунды, а длительность самого автоколебательного режима –десятки часов, определяясь временем существования градиента концентрации в растворе. (Рис.1) Полученные результаты позволяет считать перспективным использование капель ПАВ для ускорения массообменных процессов в неоднородных растворах в условиях, когда механическое перемешивание смеси невозможно.
 

Рис 1. Распределение концентрации внутри и вблизи капли ПАВ диаметром 6 мм в разные моменты цикла.

В рамках несимметричной теории упругости (среды Коссера) рассмотрена задача о распространении поверхностных акустических волн в полупространстве. Открыт качественно новый тип поверхностной волны, аналогов которой нет в классической теории упругости. Обнаруженная волна имеет три компоненты: сдвиговую, лежащую в плоскости поверхности, и две ротационные.
 

Для моделирования стадии послефильерного разбухания струи вязкоупругой жидкости предложены новый алгоритм нахождения свободной поверхности, позволивший повысить устойчивость вычислительной схемы и увеличить скорость сходимости решения, и методика обработки экспериментальных данных с использованием компьютерной технологии. Определены эффективные времена релаксации и последействия.
 

Создана методика компьютерного моделирования гидродинамических явлений в горизонтальном канале двухкомпонентной смеси, определяемых влиянием эффекта термической диффузии Людвига-Соре, на фоне конвекции гравитационного и/или вибрационного типов. На основе этой методики разработан комплекс программ, с помощью которого изучены надкритические колебательные и хаотические режимы термовибрационной конвекции.
 

Экспериментально обнаружен и изучен новый вид вибрационного взаимодействия колеблющихся в несжимаемой жидкости твердых тел, связанный с вязкими силами. Показано, что на тело, колеблющееся вблизи стенки на расстоянии вязкого взаимодействия (меньшем или сравнимом с толщиной слоя Стокса), действует сила отталкивания, проявляющаяся во всем интервале безразмерных частот. В области высоких частот за пределами вязкого взаимодействия, на расстоянии больше толщины слоя Стокса, сила отталкивания сменяется силой притяжения.
 

Предложена методика построения биортогональных вейвлет-базисов с компактным носителем (финитные функции), удовлетворяющих однородным граничным условиям. Разработан и реализован быстрый численный алгоритм, использующий биортогональные вейвлет-базисы, для решения линейных дифференциальных уравнений. Алгоритм опробован на одномерных задачах линейной теории упругости. Методика построения биортогональные вейвлетов обобщена на (неоднородные в общем случае) многомерные операторы гиперболического типа.
 

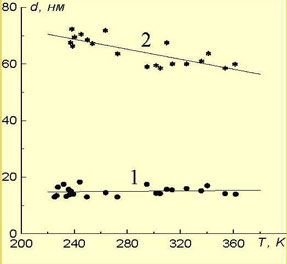
Разработан новый метод кластерного анализа магнитных жидкостей, основанный на разложении спектра динамической восприимчивости в ряд по функциям Дебая и на известной зависимости времени релаксации намагниченности от размера коллоидных частиц. В магнитных жидкостях на основе жидких углеводородов обнаружены квазисферические кластеры с некомпенсированным магнитным моментом, имеющие характерный размер 50-70 нм и включающие в себя от нескольких десятков до нескольких сотен частиц. (Рис.2)
 

Рис 2. Зависимость диаметра одиночных частиц (1) и эффективного диаметра кластеров (2) от температуры для магнитной жидкости на основе керосина.

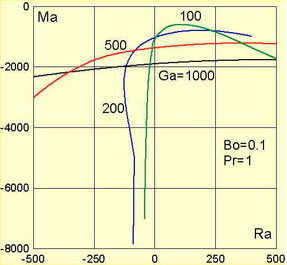
В рамках обобщенного приближения Буссинеска исследовано возникновение неустойчивости Релея-Бенара-Марангони в горизонтальном слое жидкости с деформируемой свободной поверхностью. Найдено, что плавучесть понижает устойчивость системы по отношению к монотонным длинноволновым возмущениям и, в случае нормального термокапиллярного эффекта, приводит к стабилизации деформационной моды колебательной неустойчивости, особенно сильной при малых числах Галилея. Обнаружен эффект абсолютной стабилизации релеевской неустойчивости при малых числах Галилея. (Рис.3).

Рис 3. Границы колебательной неустойчивости равновесия на плоскости параметров число Релея - число Марангони для разных чисел Галилея (кривые 1-4: 200, 500, 1000).

 (Институт механики сплошных сред).
 

Предложен метод численного решения уравнений гидромеханики для многосвязных областей, учитывающий реальную геометрию областей интегрирования и их влияние на характер течения, как для ламинарного, так и турбулентного диапазонов. Результат имеет основополагающее значение для гидромеханики. (Институт прикладной механики).
 

ФИЗИКО-ХИМИЧЕСКАЯ ГАЗОДИНАМИКА И ПРОЦЕССЫ ПРИ ВЫСОКИХ ПЛОТНОСТЯХ ЭНЕРГИИ. Созданы физико-математические модели горения твердых ракетных топлив, исследованы процессы распада в жидком слое и на поверхности раздела фаз, реакции деструкции и реструктуризации в жидко-вязком слое, показан характер взаимодействия компонентов топлив в конденсированной и газовой фазах, его влияние на характеристики энергетических установок. Полученные приоритетные данные важны для создания новых высокоэффективных ракетных топлив. (Институт прикладной механики).
 

ФИЗИКА И МЕХАНИКА ДЕФОРМИРОВАНИЯ И РАЗРУШЕНИЯ СПЛОШНЫХ СТРУКТУРИРОВАННЫХ МАТЕРИАЛОВ, В ТОМ ЧИСЛЕ, В ЭКСТРЕМАЛЬНЫХ УСЛОВИЯХ. ТРИБОЛОГИЯ. С помощью структурно-механической модели, проведено компьютерное исследование процессов развития разрушения дисперсно-наполненных эластомерных композитов. Для систем с различной степенью наполнения и прочностью эластомерной матрицы построены соответствующие деформационные зависимости дилатации композита как результат развития в нем структурной поврежденности. Установлена количественная связь между изменением объема наполненного эластомера и числом структурных микроповреждений. (Институт механики сплошных сред).
 

Построена модель, рассматривающая систему дифференциальных уравнений для описания сопротивления металла большим высокотемпературным пластическим деформациям как неравновесного процесса, в котором металл упрочняется, проявляет вязкие свойства и разупрочняется за счет динамического и статического типов возврата и динамической рекристаллизации. Предложена методика проведения экспериментов для идентификации модели. Выполнена идентификация параметров модели на базе экспериментов по сжатию цилиндрических стальных образцов при температуре 1000^оС на созданной пластометрической установке. (Институт машиноведения).
 

Разработаны научные основы управления формированием показателей качества металлопродукции методом высокотемпературной термомеханической обработки посредством моделирования процессов упрочнения. Практическое использование результатов показало повышение их долговечности в 2 – 5 раз при усталостном нагружении и в 1,5 – 2 раза при абразивном изнашивании. Результаты являются основой развития упрочняющих технологий для получения изделий с заданными характеристиками качества. (Институт прикладной механики).
 

ФИЗИКА КОНДЕНСИРОВАННЫХ СРЕД. Установлен новый тип критических явлений в конденсированных средах и кристаллической плазме – структурно-скейлинговые переходы. Исследованы термодинамика и феноменология существенно-неравновесных систем с дефектами, что позволило объяснить закономерности формирования волновых фронтов и разрушения твердых тел в широком диапазоне интенсивностей нагрузки. (Институт механики сплошных сред).
 

ФИЗИКА МАГНИТНЫХ ЯВЛЕНИЙ, МАГНИТНЫЕ МАТЕРИАЛЫ И СТРУКТУРЫ. Для суперпарамагнитной теории предложен новый высокоэффективный метод решения уравнения Фоккера-Планка (уравнение Брауна). Область применимости метода — низкотемпературный предел, где все стандартные способы решения сталкиваются со значительными трудностями. Новый подход позволяет радикально сократить объем вычислений и гарантирует их сходимость. Для иллюстрации, решена задача о динамическом гистерезисе одноосной магнитной частицы и впервые получены результаты для безразмерных высот потенциального барьера порядка 100 и выше.
 

Полностью решен вопрос о пределах применимости в теоретической микрореологии так называемого безынерционного приближения – пренебрежения моментом инерции тестовой частицы при описании ее вращения. В допустимой области продемонстрированы расчетные возможности безынерционного предела: найдены полевые зависимости эффективных времен продольной и поперечной магнито-ориентационной релаксации частицы и исследовано влияние поля на сдвиговую вязкость суспензии таких частиц. (Институт механики сплошных сред).
 

ВЗАИМОДЕЙСТВИЕ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ, В ТОМ ЧИСЛЕ В СВЕРХСИЛЬНЫХ ПОЛЯХ. Разработан быстродействующий широкополосный фотоприемник мощного лазерного излучения, работающий на нелинейном эффекте оптического выпрямления в нанографитной пленке. Фотоприемник функционирует без внешнего источника питания, обеспечивает регистрацию лазерных импульсов в широком спектральном диапазоне (от 0,266 до 5 мкм) с быстродействием менее 0,5 нс, а его чувствительность на длине волны 1 мкм составляет 500 мВ/МВт. Фотоприемник нового типа найдет широкое применение, в том числе в ракетно-космической технике. (Институт прикладной механики).
 

СУПРАМОЛЕКУЛЯРНЫЕ И НАНОРАЗМЕРНЫЕ САМООРГАНИЗУЮЩИЕСЯ СИСТЕМЫ ДЛЯ ИСПОЛЬЗОВАНИЯ В СОВРЕМЕННЫХ ВЫСОКИХ ТЕХНОЛОГИЯХ. Исследованы закономерности упорядочения и самоорганизации систем наночастиц и разработан метод расчета этих процессов с использованием потенциала парного взаимодействия элементов наноструктуры, учитывающего силы и моменты сил. Метод открывает возможность моделирования эволюционных процессов, протекающих в нанопорошковых композитах при их формировании и эксплуатации. (Институт прикладной механики).
 

Методом молекулярной динамики выявлены закономерности процессов поглощения, хранения и выделения водорода фуллеритами в зависимости от формы, структуры и размера фуллеренов, входящих в наноструктуру, при переменных термодинамических параметрах. Результаты исследований важны для создания нового поколения аккумуляторов водорода и развития водородной энергетики. (Институт прикладной механики).
 

Отчет о научной и научно-организационной
деятельности за 2005 г. Часть 1.